Kapilaritātes īpašības un piemērs ūdenī
The kapilaritāte Tas ir šķidrumu īpašība, kas ļauj tiem pārvietoties caur cauruļveida caurumiem vai porainām virsmām pat pret gravitācijas spēku. Šim nolūkam ir jābūt līdzsvaram un divu spēku koordinācijai, kas saistīti ar šķidrajām molekulām: kohēzija un saķere; kam ir šīs divas fiziskas pārdomas, ko sauc par virsmas spriegumu.
Šķidrumam ir jāspēj mitrināt caurules iekšējās sienas vai materiāla poras, caur kurām tas pārvietojas. Tas notiek, ja saķeres spēks (kapilārā caurules šķidruma siena) ir lielāks nekā starpmolekulārā kohēzijas spēks. Līdz ar to šķidrās molekulas rada spēcīgāku mijiedarbību ar materiāla atomiem (stikls, papīrs utt.) Nekā starp tām.
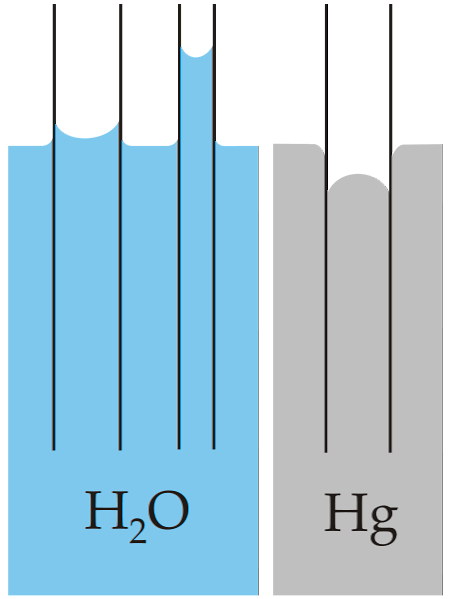
Klasiskais kapilaritātes piemērs ir parādīts salīdzinot šo īpašību divos ļoti atšķirīgos šķidrumos: ūdenī un dzīvsudrabā.
Augšējais attēls rāda, ka ūdens palielinās caur caurules sienām, kas nozīmē, ka tam ir augstāki saķeres spēki; kamēr dzīvsudrabs ir pretējs, jo tā savienojamie, metāliskie savienojumi neļauj to mitrināt.
Šā iemesla dēļ ūdens veido ieliektu menisku, un dzīvsudrabs ir izliekts menisks (kupola formas). Jāatzīmē, ka jo mazāks ir caurules rādiuss vai sekcija, caur kuru šķidrums pārvietojas, jo lielāks ir augstums vai nobrauktais attālums (salīdziniet abu cauruļu ūdens kolonnu augstumus).
Indekss
- 1 Kapilaritātes raksturojums
- 1.1 - Šķidruma virsma
- 1.2. Augstums
- 1.3. Virsmas spriedze
- 1.4. Kapilāra vai poru, kur šķidrums palielinās, rādiuss
- 1,5 - kontakta leņķis (θ)
- 2 Ūdens kapilaritāte
- 2.1 Uz augiem
- 3 Atsauces
Kapilaritātes raksturojums
-Šķidruma virsma
Šķidruma virsma, ti, ūdens, kapilārā ir ieliekta; tas ir, menisks ir ieliekts. Šāda situācija rodas tāpēc, ka to spēku ietekme uz ūdens molekulām, kas atrodas pie caurules sienas, ir vērsta uz to.
Visā meniskā ir saskares leņķis (θ), kas ir leņķis, kas veido kapilārā caurules sienu ar līnijas pieskari šķidruma virsmai saskares punktā..
Adhēzijas un kohēzijas spēki
Ja šķidruma adhēzijas spēks kapilārā sienā dominē pār starpmolekulārās kohēzijas spēku, tad leņķis ir θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
Kad tīrā stikla virsmā tiek ievietots ūdens piliens, uz stikla plūst ūdens, lai θ = 0 un cos θ = 1.
Ja starpmolekulārā kohēzijas spēks dominē virs kapilāra šķidruma sienas saķeres stiprības, piemēram, dzīvsudrabā, menisks būs izliekts un leņķis value būs lielāks par 90º; dzīvsudrabs neiztērē kapilāro sienu un tādējādi nokrīt caur iekšējo sienu.
Ja uz tīra stikla virsmas ievieto dzīvsudraba pilienu, piliens saglabā savu formu un leņķis θ = 140º.
-Augstums
Ūdens caur kapilāro cauruli sasniedz augstumu (h), kurā ūdens kolonnas svars kompensē starpmolekulārās kohēzijas spēka vertikālo komponentu..
Tā kā palielinās ūdens daudzums, būs vieta, kur gravitācija pārtrauks tās celšanos, pat ar virsmas spriegumu, kas darbojas jūsu labā.
Kad tas notiek, molekulas nevar turpināt "uzkāpt" iekšējām sienām, un visi fiziskie spēki tiek izlīdzināti. No vienas puses, jums ir spēki, kas veicina ūdens pieaugumu, un, no otras puses, jūsu pašu svars to nospiež.
Jurina likums
To var rakstīt matemātiski šādi:
2 π rΥcosθ = ρgπr2h
Ja vienādojuma kreisā puse ir atkarīga no virsmas spriedzes, kuras lielums ir saistīts arī ar kohēzijas vai starpmolekulārajiem spēkiem; Cosθ ir kontakta leņķis un r cauruma rādiuss, caur kuru šķidrums palielinās.
Un vienādojuma labajā pusē ir augstums h, smaguma spēks g un šķidruma blīvums; tas būtu ūdens.
Tīrīšana, tad jums ir
h = (2Υcosθ / ρgr)
Šis formulējums ir pazīstams kā Jurin likums, kas nosaka augstumu, ko sasniedz šķidruma kolonna kapilārā caurulē, kad šķidruma kolonnas svars ir līdzsvarots ar pacelšanās spēku ar kapilāru..
-Virsmas spriedze
Ūdens ir dipolāra molekula, ko izraisa skābekļa atoma un molekulārās ģeometrijas elektronegativitāte. Tas izraisa to, ka ūdens molekulas daļa, kurā atrodas skābeklis, ir negatīvi lādēta, bet ūdens molekulas daļa, kas satur 2 ūdeņraža atomus, ir pozitīvi uzlādēta..
Šķidruma molekulas mijiedarbojas, pateicoties vairākām ūdeņraža saitēm, saglabājot tās kopā. Tomēr ūdens molekulas, kas atrodas saskarnes ūdenī: gaisā (virsmā), ir šķidruma sinusa molekulu neto pievilcība, ko nespēj kompensēt vājā piesaiste ar gaisa molekulām..
Tāpēc saskarnes ūdens molekulas tiek pakļautas pievilcīgam spēkam, kas mēdz noņemt ūdens molekulas no saskarnes; tas ir, ūdeņraža tilti, kas veidojas ar apakšā esošajām molekulām, kuras atrodas uz virsmas. Tādējādi virsmas spriedze cenšas samazināt ūdens virsmu: gaisa saskarni.
Saistība ar h
Ja paskatās Jurina likuma vienādojumu, jūs atradīsiet, ka h ir tieši proporcionāls Υ; tādēļ, jo lielāks šķidruma virsmas spriegums, jo lielāks ir augstums, kas var pieaugt caur kapilāru vai materiāla porām.
Tādējādi var sagaidīt, ka diviem šķidrumiem, A un B ar dažādiem virsmas spriegumiem, tas, kuram ir visaugstākā virsmas spriedze, palielinās līdz augstākam augstumam.
No šī punkta var secināt, ka augsta virsmas spriedze ir vissvarīgākā īpašība, kas nosaka šķidruma kapilāro īpašību.
-Kapilāra vai poru rādiuss, kur šķidrums palielinās
Jurīna likuma ievērošana norāda, ka augstums, ko sasniedz šķidrums kapilārā vai porās, ir apgriezti proporcionāls tā paša rādiusam..
Tāpēc, jo mazāks rādiuss, jo lielāks ir augstums, ko šķidruma kolonna sasniegs ar kapilāru darbību. To var redzēt tieši attēlā, kur ūdeni salīdzina ar dzīvsudrabu.
Stikla caurulē, kuras rādiuss ir 0,05 mm, ūdens kolonna ar kapilaritāti sasniegs 30 cm augstumu. Kapilārcaurulēs, kuru rādiuss ir 1 μm ar iesūkšanas spiedienu 1,5 x 103 hPa (kas ir vienāds ar 1,5 atm) atbilst ūdens kolonnas augstuma aprēķinam no 14 līdz 15 m.
Tas ir ļoti līdzīgs tam, kas notiek ar salmiem, kas paši vairākkārt griežas. Nogatavinot šķidrumu, rodas spiediena starpība, kas izraisa šķidruma iekļūšanu mutē.
Maksimālā augstuma vērtība kolonnai, ko sasniedz kapilaritāte, ir teorētiska, jo kapilāru rādiusu nevar samazināt, pārsniedzot noteiktu robežu.
Poiseuila likums
Tas nosaka, ka reālā šķidruma plūsmu izsaka šādi:
Q = (πr4/ 8ηl) ΔP
Ja Q ir šķidruma plūsma, η ir tā viskozitāte, l caurules garums un ΔP spiediena starpība.
Samazinot kapilāra rādiusu, šķidruma kolonnas augstumam, kas sasniegts ar kapilaritāti, vajadzētu palielināties uz nenoteiktu laiku. Tomēr Poiseuille norāda, ka rādiusa samazināšana samazina arī šķidruma plūsmu caur šo kapilāru.
Turklāt viskozitāte, kas ir pretestības mērs, kas iebilst pret īsta šķidruma plūsmu, vēl vairāk samazinātu šķidruma plūsmu..
-Kontakta leņķis (θ)
Jo augstāka ir cosθ vērtība, jo augstāks ir ūdens kolonnas augstums ar kapilaritāti, kā to norāda Jurin likums.
Ja θ ir mazs un tuvojas nullei (0), cosθ ir = 1, tāpēc vērtība h būs maksimāla. Gluži pretēji, ja θ ir vienāds ar 90º, cosθ = 0 un h = 0 vērtība.
Ja θ vērtība ir lielāka par 90º, kas ir izliekta meniska gadījumā, šķidrums nepalielinās ar kapilaritāti un tās tendence ir nolaišanās (kā tas notiek ar dzīvsudrabu)..
Ūdens kapilaritāte
Ūdens virsmas spraiguma vērtība ir 72,75 N / m, salīdzinoši augsta, salīdzinot ar šādu šķidrumu virsmas sprieguma vērtībām:
-Acetons: 22,75 N / m
-Etilspirts: 22,75 N / m
-Heksāns: 18,43 N / m
-Metanols: 22,61 N / m.
Tāpēc ūdenim ir ārkārtēja virsmas spriedze, kas veicina tādu kapilāru parādības attīstību, kas ir nepieciešama ūdens un barības vielu uzsūkšanai augos..
Uz augiem

Kapilaritāte ir svarīgs mehānisms, lai palielinātu sula ar augu xilēmu, bet tas pats par sevi nav pietiekams, lai sula sasniegtu koku lapas..
Caurplūdums vai iztvaikošana ir svarīgs mehānisms auga pacelšanai ar augu ksilēmu. Lapas zaudē ūdeni, iztvaicējot, samazinot ūdens molekulu daudzumu, kas izraisa kapilāru caurulēs esošo ūdens molekulu piesaisti (xylem)..
Ūdens molekulas nedarbojas viens no otra, bet mijiedarbojas ar Van der Waals spēkiem, kas liek viņiem pacelties, ko ar augu kapilāru caurulēm savieno ar lapām..
Papildus šiem mehānismiem jāatzīmē, ka augi absorbē ūdeni no augsnes osmozes veidā un ka saknes radītais pozitīvais spiediens virza ūdens pacelšanās sākumu caur iekārtas kapilāriem..
Atsauces
- García Franco A. (2010). Virsmas parādības. Saturs iegūts no: sc.ehu.es
- Virsmas parādības: virsmas spraigums un kapilaritāte. [PDF] Saturs iegūts no: ugr.es
- Vikipēdija. (2018). Kapilārums Saturs iegūts no: en.wikipedia.org
- Risvhan T. (s.f.) Kapilaritāte augos. Saturs iegūts no: academia.edu
- Helmenstine, Anne Marie, Ph.D. (2018. gada 22. decembris). Kapilārā darbība: definīcija un piemēri. Saturs iegūts no: thinkco.com
- Ellen Ellis M. (2018). Ūdens kapilārā darbība: definīcija un piemēri. Pētījums. Saturs iegūts no: study.com
- ScienceStruck personāls. (2017. gada 16. jūlijs). Piemēri, kas izskaidro kapilāro darbību koncepciju un nozīmi. Saturs iegūts no: sciencestruck.com


