Cik simetrijas asīm ir aplis?

The apļa simetrijas asis Tie ir bezgalīgi. Šīs asis ir tādas, kas sadala jebkuru ģeometrisko formu divās tieši vienādās daļās.

Un aplis sastāv no visiem punktiem, kuru attālums līdz fiksētam punktam ir mazāks vai vienāds ar noteiktu vērtību "r".

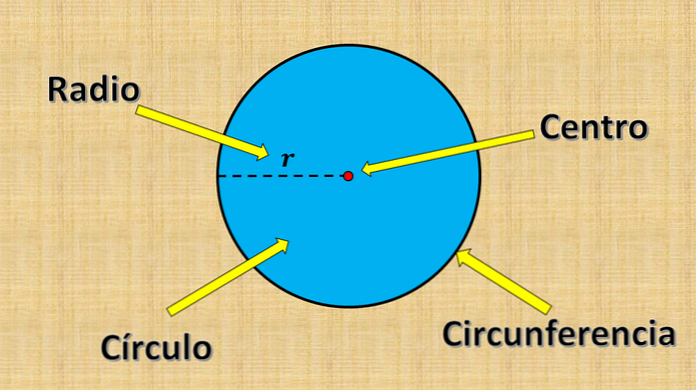
Iepriekš minēto fiksēto punktu sauc par centru, un vērtību "r" sauc par rādiusu. Rādiuss ir lielākais attālums, kas var būt starp punktu apli un centru.

No otras puses, jebkuru līnijas segmentu, kura galiņi atrodas apļa malā (apkārtmērs) un šķērso centru, sauc par diametru. Tā mērījums vienmēr ir vienāds ar divkāršu rādiusu.

Aplis un apkārtmērs

Nesajauciet apli ar apli. Apkārtmērs attiecas tikai uz punktiem, kas atrodas attāluma "r" attālumā no centra; tas ir, tikai apļa mala.

Tomēr, meklējot simetrijas asīm, tas ir vienaldzīgs, ja strādājat ar apli vai ar apli.

Kas ir simetrijas ass?

Simetrijas ass ir līnija, kas divās vienādās daļās sadala noteiktu ģeometrisko figūru. Citiem vārdiem sakot, simetrijas ass darbojas kā spogulis.

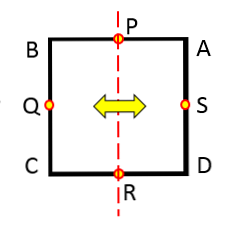
Apļa simetrijas asis

Ja jūs novērojat jebkuru apli, neatkarīgi no tā rādiusa, jūs varat redzēt, ka ne katra līnija, kas šķērso to, ir simetrijas ass.

Piemēram, neviena no šādā attēlā iezīmētajām līnijām nav simetrijas ass.

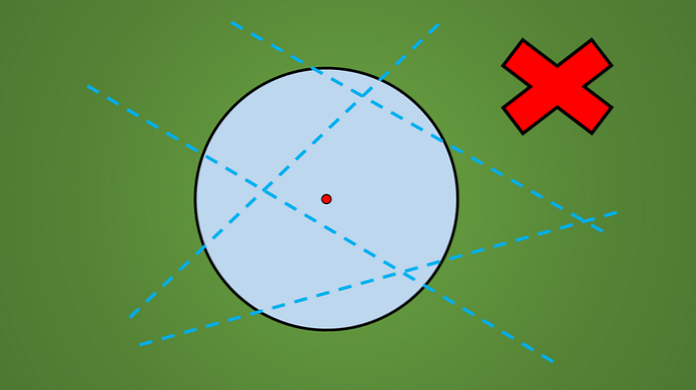
Vienkāršs veids, kā pārbaudīt, vai līnija ir simetrijas ass, vai ne, ir perpendikulāri ģeometriskajam attēlam uz līnijas pretējo pusi..

Ja atstarojums neatbilst oriģinālajam skaitlim, tad šī līnija nav simetrijas ass. Šis paņēmiens ilustrē šo attēlu.

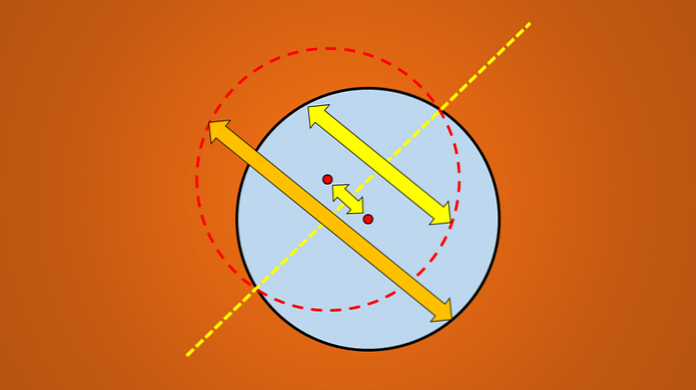
Bet, ja tiek ņemts vērā šāds attēls, ir labi zināms, ka līnija ir apļa simetrijas ass.

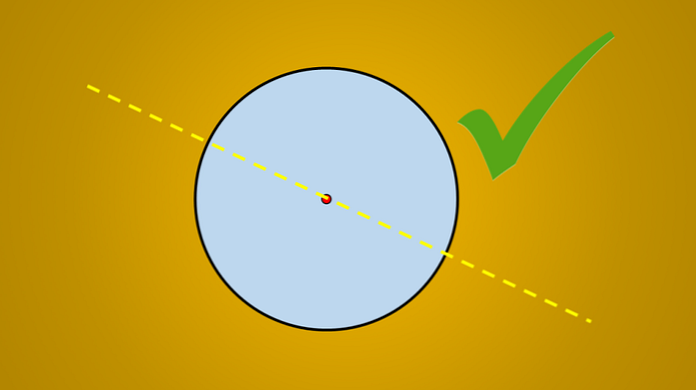
Jautājums ir: vai ir vairāk simetrijas asu? Atbilde ir „jā”. Ja jūs pagriežat šo līniju 45 ° pretēji pulksteņrādītāja virzienam, iegūtā līnija ir arī apļa simetrijas ass.

Tas pats notiek, ja jūs pagriežat 90 °, 30 °, 8 ° un, vispār, jebkādu grādu skaitu.

Svarīga lieta par šīm līnijām ir nevis slīpums, kas viņiem ir, bet tās visas iet cauri apļa centram. Tāpēc jebkura līnija, kas satur apļa diametru, ir simetrijas ass.

Tātad, tā kā lokam ir bezgalīgs diametru skaits, tad tam ir bezgalīgs simetrijas asu skaits..

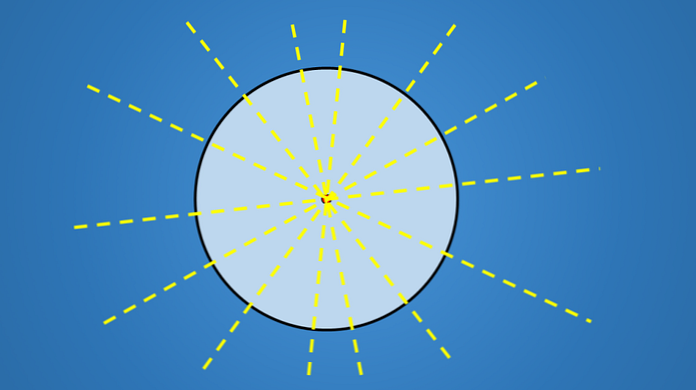
Citiem ģeometriskiem attēliem, piemēram, trijstūrim, četrstūrim, piecstūrim, sešstūrim vai jebkuram citam daudzstūrim, ir ierobežots simetrijas asu skaits..

Iemesls, kāpēc lokam ir neierobežots simetrijas asu skaits, ir tas, ka tai nav sānu.

Atsauces

1. Basto, J. R. (2014). Matemātika 3: Analītiskā ģeometrija. Patria Redakcijas grupa.
2. Billstein, R., Libeskind, S., &, Lott, J., W., (2013). Matemātika: problēmu risināšanas pieeja pamatizglītības skolotājiem. López Mateos Editores.
3. Bult, B., un Hobbs, D. (2001). Matemātikas leksikons (ilustrēts red.). (F. P. Cadena, Trad.) Izdevumi AKAL.
4. Callejo, I., Aguilera, M., Martinez, L., un Aldea, C. (1986). Matemātika Ģeometrija E.G.B augstākā cikla reforma. Izglītības ministrija.
5. Schneider, W., & Sappert, D., (1990). Praktiskā tehniskā rasējuma rokasgrāmata: ievads rūpnieciskās tehniskās rasēšanas pamatos. Reverte.
6. Thomas, G. B., un Weir, M. D. (2006). Aprēķins: vairāki mainīgie. Pearson Education.