Arhimēda biogrāfija, iemaksas un izgudrojumi
Arhimēda no Sirakūzas (287 a.C - 212 a.C) bija matemātiķis, fiziķis, izgudrotājs, inženieris un grieķu astronoms no senās Sirakūzas pilsētas Sicīlijas salā. Viņa izcilākie ieguldījumi ir Arhimēda princips, izsvītrojuma metodes izstrāde, mehāniskā metode vai pirmās planetārijas izveide..
Šobrīd to uzskata par vienu no trīs svarīgākajiem senatnes matemātikas rādītājiem, kas atrodas blakus Euclides un Apolonio, jo tās ieguldījums nozīmīgi nozīmīgi zinātnes sasniegumi šajā laikā aprēķinu, fizikas, ģeometrijas un astronomijas jomās. Tas savukārt padara viņu par vienu no izcilākajiem zinātniekiem cilvēces vēsturē.

Lai gan ir zināmas dažas viņa personīgās dzīves detaļas, un tās, kas ir zināmas, ir apšaubāmas, viņa iemaksas ir zināmas, pateicoties virknei rakstisku vēstuļu par viņa darbiem un sasniegumiem, kas saglabājušies līdz mūsdienām, kas piederēja līdz mūsdienām. uz saraksti, ko viņš gadiem ilgi uzturēja ar draugiem un citiem matemātiķiem.
Arhimēda savā laikā bija slavena ar saviem izgudrojumiem, kas piesaistīja viņa laikabiedru uzmanību, daļēji tāpēc, ka tie tika izmantoti kā kara līdzekļi, lai veiksmīgi izvairītos no daudziem romiešu iebrukumiem..
Tomēr ir teikts, ka viņš apgalvoja, ka vienīgā ļoti svarīgā lieta bija matemātika un ka viņa izgudrojumi bija tikai piemērota ģeometrijas spēle. Pēctečiem viņa darbi tīrā matemātikā ir daudz vērtīgāki nekā viņa izgudrojumi.
Indekss
- 1 Biogrāfija
- 1.1 Apmācība
- 1.2. Zinātniskais darbs
- 1.3. Konflikts Sirakūzā
- 1.4 Nāve
- 2 Arhimēda zinātniskais ieguldījums
- 2.1 Arhimēda princips
- 2.2 Mehāniskā metode
- 2.3. Sviras likuma skaidrojums
- 2.4. Izpētes vai izsīkuma metodes izstrāde zinātniskajai demonstrācijai
- 2.5 Apļa mērs
- 2.6 Sfēru un cilindru ģeometrija
- 3 Izgudrojumi
- 3.1. Odometrs
- 3.2 Pirmais planetārijs
- 3.3 Arhimēda skrūve
- 3.4 Arhimēda kārta
- 4 Atsauces
Biogrāfija
Arhimēda no Sirakūzas dzimusi aptuveni 287. gadā pirms mūsu ēras. Nav daudz informācijas par viņa pirmajiem gadiem, lai gan var teikt, ka viņš ir dzimis Sirakūzā, pilsētā, kas šodien tiek uzskatīta par Sicīlijas salas galveno ostu Itālijā..
Toreiz Syracuse bija viena no pilsētām, kas veidoja tā saukto Magna Greciju, kas bija Grieķijas izcelsmes kolonistu vieta Itālijas un Sicīlijas pussalas dienvidu daļā..
Nav zināmi fakti par Archimedes māti. Saistībā ar tēvu ir zināms, ka to sauca par Phidias un ka viņš bija veltīts astronomijai. Šī viņa tēva informācija ir zināma, pateicoties grāmatas fragmentam Smilšu skaitītājs, rakstījis Archimedes, kurā viņš piemin savu tēva vārdu.
Heraklīds, kurš bija grieķu filozofs un astronoms, ļoti iepriecināja Arhimēdi un pat par viņu rakstīja biogrāfiju. Tomēr šis dokuments nav saglabāts, tāpēc visa tajā esošā informācija nav zināma.
No otras puses, vēsturnieks, filozofs un biogrāfs Plutarco savā grāmatā ar nosaukumu Parallel Lives norādīja, ka Arhimēdam bija asins attiecības ar Hiero II, tirānu, kurš kopš 26. gada pirms mūsu ēras bija Sirakūzā..
Apmācība
Tā kā mums ir neliela informācija par Arhimēda, mēs nezinām, kur viņš ieguva pirmo apmācību.
Tomēr dažādi historiogrāfi ir konstatējuši, ka pastāv liela iespēja, ka Archimedes studējis Aleksandrijā, kas bija vissvarīgākais Grieķijas kultūras un mācību centrs šajā reģionā..
Šo pieņēmumu pamato Grieķijas vēsturnieka Diodoro Sículo sniegtā informācija, kas norādīja, ka Arhimēds, iespējams, studējis Aleksandrijā.
Turklāt daudzos viņa darbos Archimedes pats piemin citus zinātniekus no tā laika, kura darbs bija koncentrēts Aleksandrijā, tāpēc var pieņemt, ka viņš faktiski ir attīstījies šajā pilsētā..
Dažas no personībām, ar kurām domājams, ka Aleksandrijā mijiedarbojas, ir ģeogrāfi, matemātiķis un astronoms Eratostens no Kirēnas un matemātiķis un astronoms Conon de Sanos.
Ģimenes motivācija
No otras puses, fakts, ka Arhimēda tēvs bija astronoms, varēja būtiski ietekmēt viļņus, ko viņš vēlāk parādīja, jo vēlāk un no maziem bērniem īpaša pievilcība bija vērojama šajā jomā. zinātnes.
Pēc viņa laika Aleksandrijā tiek lēsts, ka Arhimēds atgriezās Sirakūzā.
Zinātniskais darbs
Pēc atgriešanās Syracuse, Archimedes sāka izstrādāt dažādus artefaktus, kas drīz ieguva viņam zināmu popularitāti šīs pilsētas iedzīvotāju vidū. Šajā laika posmā viņš sevi pilnībā pauda zinātniskajam darbam, ražoja dažādus izgudrojumus un secināja vairākus matemātiskus priekšstatus, kas bija ļoti progresīvi.
Piemēram, kad viņš veltīja sevi cietu izliektu un plakanu figūru raksturojumu izpētei, viņš nāca klajā ar koncepcijām, kas saistītas ar integrālo un diferenciālo aprēķinu, kas tika izstrādāts vēlāk.
Arhimēda arī noteica, ka tilpums, kas saistīts ar sfēru, atbilst divreiz lielākam cilindra lielumam, un tas bija tas, kurš izgudroja kompozīta skriemeli, pamatojoties uz viņa atklājumiem par sviras likumu..
Konflikts Sirakūzā
213.gadā pirms mūsu ēras Romas karavīri ieradās Sirakūzas pilsētā un ieskauj apmetējus, lai tos nodotu.
Šo darbību vadīja militārais un grieķu politiķis Marco Claudio Marcelo Otrā Puniskā kara ietvaros. Vēlāk tas bija pazīstams kā Romas zobens, jo tas beidzot iekaroja Sirakūzu.
Konflikta vidū, kas ilga divus gadus, Sirakūzas iedzīvotāji cīnījās pret romiešiem ar drosmi un drosmi, un Archimedes spēlēja ļoti svarīgu lomu, ņemot vērā, ka viņš ir veltījis instrumentus un instrumentus, kas palīdzēja uzvarēt romiešus.
Visbeidzot, Marco Claudio Marcelo pārņēma Sirakūzas pilsētu. Pirms Lielās Arhimēda intelektualitātes Marcelo pavēlēja, lai viņi netiktu ievainoti vai nogalināti. Tomēr Arhimēds tika nogalināts romiešu kareivja rokās.
Nāve
Arhimēda nomira 212. gadā pirms mūsu ēras. Vairāk nekā 130 gadus pēc viņa nāves 137. gadā pirms mūsu ēras rakstnieks, politiķis un filozofs Marco Tulio Cicero ieņēma pozīciju Romas pārvaldē un vēlējās atrast Archimedes kapu.
Šis uzdevums nebija viegls, jo Cicero nevarēja atrast nevienu, kas norādītu precīzu vietu. Tomēr viņš galu galā ieguva to ļoti tuvu Agrigento durvīm un nožēlojamos apstākļos.
Cicero iztīra kapu un atklāja, ka cilindra iekšpusē tas bija uzrakstīts ar sfēru, kas ir atsauce uz atklājumu par Archimedes pirms kāda laika..
Versijas par viņa nāvi
Pirmā versija
Vienā no versijām teikts, ka Arhimēda atradās matemātiskas problēmas risināšanā, kad viņš bija ieradies ar romiešu karavīru. Ir teikts, ka Arhimēds kādu laiku varētu lūgt viņam atrisināt šo problēmu, tāpēc karavīrs viņu būtu nogalinājis.
Otra versija
Otrā versija ir līdzīga pirmajai versijai. Ņemiet vērā, ka Archimedes atrisināja matemātikas problēmu, kad notika pilsēta.
Romiešu kareivis ienāca viņa savienojumā un lika viņam tikties ar Marcelo, un Archimedes atbildēja, ka viņam ir jārisina problēma, ar kuru viņš strādāja. Karavīrs izjaucās šīs atbildes rezultātā un nogalināja viņu.
Trešā versija
Šī hipotēze liecina, ka Arhimēda rokās bija ļoti daudz matemātikai raksturīgu instrumentu. Tad karavīrs viņu redzēja, un viņš domāja, ka viņam varētu būt vērtīgi priekšmeti, tāpēc viņš viņu nogalināja.
Ceturtā versija
Šī versija ilustrē, ka Arhimēda bija grumba pie zemes, domājot par plāniem, ko viņš mācīja. Acīmredzot romiešu kareivis nāca no aizmugures un, neapzinoties, ka tas bija Arhimēds, viņu nošāva.
Arhimēda zinātniskie ieguldījumi
Arhimēda princips
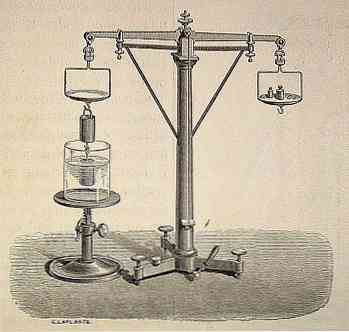
Arhimēda principu mūsdienu zinātne uzskata par vienu no svarīgākajiem senā laikmeta mantojumiem.
Visā vēsturē un mutiski, ir ziņots, ka Arhimēds nejauši atnāca pie viņa, pateicoties karaļam Hieronam, kurš bija pasūtījis, lai redzētu, vai zelta kronis, ko viņš nosūtījis ražot, bija tikai zelts tīra un nesaturēja citu metālu. Man tas bija jāveic, neiznīcinot vainagu.
Ir teikts, ka, Archimedes meditējot, kā atrisināt šo problēmu, viņš nolēma peldēties, un, kad viņš ieradās vannā, viņš saprata, ka ūdens palielinās līmenī, kad viņš iegremdējās tajā..
Šādā veidā viņš atklās zinātnisko principu, ka "katrs ķermenis, kas pilnībā vai daļēji iegremdēts šķidrumā (šķidrums vai gāze), saņem augšupejošu vilces spēku, kas ir vienāds ar objekta novadītā šķidruma svaru"..
Šis princips nozīmē, ka šķidrumi uzspiež augšup vērstos spēkus uz visiem iegremdētajiem objektiem un ka šī stumšanas spēka daudzums ir vienāds ar iegremdētā ķermeņa pārvietotā šķidruma svaru neatkarīgi no tā svara..
Šī principa skaidrojums apraksta flotācijas fenomenu, un tas ir atrodams tā Līgums par peldošām struktūrām.
Arhimēda princips ir lielā mērā izmantots pēctečiem masveida izmantošanas objektu, piemēram, zemūdens, kuģu, glābēju un balonu, peldēšanai..
Mehāniskā metode
Vēl viens no svarīgākajiem Archimedes ieguldījumiem zinātnē bija tīri mehāniskas, tas ir, tehniskas metodes iekļaušana ģeometrisko problēmu argumentācijā un argumentācijā, kas nozīmēja vēl nebijušu veidu, kā atrisināt šāda veida problēmas..
Arhimēda kontekstā ģeometrija tika uzskatīta tikai par teorētisku zinātni, un parastā lieta bija tāda, ka tīra matemātika bija vērsta uz citām praktiskajām zinātnēm, kurās varētu izmantot tās principus..
Šā iemesla dēļ šodien tā tiek uzskatīta par mehānikas kā zinātnes disciplīnas priekšteci.
Rakstā, kurā matemātiķis atklāj jauno metodi savam draugam Eratosthenes, norāda, ka tas ļauj risināt matemātikas jautājumus, izmantojot mehāniku, un ka ir nedaudz vieglāk izveidot ģeometriskas teorēmas demonstrējumu, ja tas jau ir ir dažas iepriekšējas praktiskas zināšanas, ka, ja jums nav nekādu priekšstatu par to.
Šī jaunā metode, ko Archimedes veica, kļūtu par modernās zinātniskās metodes atklāšanas un hipotēzes formālās neformālās stadijas priekšteci..
Sviras likuma skaidrojums
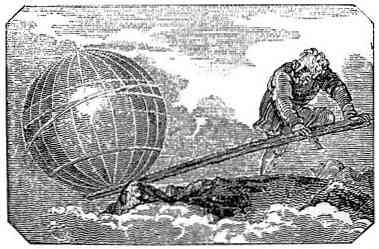
Kaut arī svira ir vienkārša mašīna, kas tika izmantota kopš daudz agrāk nekā Arhimēda, tas bija viņš, kurš formulēja principu, kas izskaidro savu darbību savā traktātā Par lidmašīnu līdzsvaru.
Šā likuma formulējumā Archimedes nosaka principus, kas apraksta sviras atšķirīgo uzvedību, novietojot tajā divas korpusus, atkarībā no tā svara un attāluma no atbalsta punkta..
Šādā veidā viņš norāda, ka divas virsmas, kuras var izmērīt (samērīgas), kas atrodas uz sviras, ir līdzsvarotas, ja tās atrodas attālumos, kas ir apgriezti proporcionāli to svaram..
Tādā pašā veidā neizmērojami ķermeņi (ko nevar izmērīt) to dara, bet šo likumu varēja pierādīt tikai Archimedes tikai ar pirmā tipa ķermeņiem..
Tā formulējums sviras principam ir labs piemērs mehāniskās metodes pielietošanai, jo, saskaņā ar tā skaidrojumu vēstulē, kas vērsta pret Dositeo, šī metode tika atklāta pirmajā brīdī, izmantojot mehānikas metodes, kas praksē tika ieviestas..
Vēlāk viņš tos formulēja, izmantojot ģeometrijas metodes (teorētiskās). No šī eksperimenta uz ķermeņiem tika noņemts arī smaguma centra jēdziens.
Izpētes vai izsmelšanas metodes izstrāde zinātniskajai demonstrācijai
Izplūde ir metode, ko izmanto ģeometrijā, kas sastāv no ģeometrisko figūru tuvināšanas, kuru laukums ir zināms ar uzrakstu un apzīmējumu, citā, kuras laukums ir paredzēts..
Lai gan Arhimēds nebija šīs metodes radītājs, viņš to meistarīgi attīstīja, spējot ar tā palīdzību aprēķināt precīzu Pi vērtības vērtību..
Arhimēda, izmantojot izsmidzināšanas metodi, uzrakstītos un ierobežotos sešstūrus ar diametra 1 diametru, samazinot līdz absurdam starpību starp sešstūru laukumu un apkārtmēru..
Lai to izdarītu, viņš šķērsoja sešstūrus, veidojot poligonus līdz pat 16 pusēm, kā parādīts iepriekšējā attēlā.
Tādā veidā viņš nāca precizēt, ka pi vērtība (attiecības starp apļa garumu un tā diametru) ir starp vērtībām 3.14084507 ... un 3.14285714 ... .
Arhimēda meistarīgi izmantoja exhaución metodi, jo ne tikai izdevās tuvināt Pi vērtības aprēķinu ar kļūdas rezervi, bet gan ļoti vēlamu, un tāpēc arī tāpēc, ka Pi ir neracionāls skaitlis, caur šī metode un iegūtie rezultāti noteica pamatus, kas dīgstos bezgalīgajā aprēķina sistēmā, un vēlāk, mūsdienu integrētajā aprēķinā..
Apļa mērs
Lai noteiktu apļa laukumu, Archimedes izmantoja metodi, kas veidoja kvadrātu, kas precīzi atbilst lokam.
Zinot, ka laukuma laukums bija tās malas summa un ka apļa platība bija lielāka, viņš sāka strādāt pie aptuvenām vērtībām. Viņš to izdarīja, nomainot laukumu ar 6-sānu poligonu un pēc tam strādājot ar sarežģītākiem daudzstūriem.
Arhimēda bija pirmais vēstures matemātiķis, lai veiktu nopietnu skaitļa Pi aprēķinu.
Sfēru un cilindru ģeometrija
No deviņiem Arhimēda darbiem matemātikā un fizikā apkopoti divi sfēras un balonu ģeometrijas apjomi..
Šis darbs attiecas uz noteikšanu, ka jebkura rādiusa sfēras virsma ir četras reizes lielāka par tās lielāko apli, un sfēras tilpums ir divas trešdaļas no tā cilindra, kurā tas ir ierakstīts.
Izgudrojumi
Odometrs
Pazīstams arī kā kilometri, tas bija šī slavenā cilvēka izgudrojums.
Šī ierīce tika uzbūvēta, pamatojoties uz riteņa principu, kas, ieslēdzot, aktivizē pārnesumus, kas ļauj aprēķināt nobraukto attālumu..
Saskaņā ar šo pašu principu, Arhimēda izstrādāja vairāku veidu odometrus militāriem un civiliem mērķiem.
Pirmais planetārijs
Pamatojoties uz daudzu klasisko rakstnieku, piemēram, Cicero, Ovid, Claudian, Marciano Capela, Casiodoro, Sexto Empirico un Lactantius, liecībām, daudzi zinātnieki tagad piešķir Archimedes pirmajam sākumlapu planetārijam.
Tas ir mehānisms, ko veido virkne "sfēru", kas spēja atdarināt planētu kustību. Līdz šim šī mehānisma detaļas nav zināmas.
Pēc Cicero domām, Arhimēda būvētie planetāriji bija divi. Vienā no tām bija pārstāvēta zeme un tās tuvumā esošās dažādās zvaigznes.
Otrā, ar vienu rotāciju, saule, mēness un planētas radīja neatkarīgas kustības attiecībā pret fiksētajām zvaigznēm tāpat kā reālajā dienā. Pēdējā gadījumā varēja novērot secīgus Mēness fāzes un aiztures.
Arhimēda skrūve
Arhimēda skrūve ir ierīce, ko izmanto, lai transportētu ūdeni no apakšas uz augšu caur slīpumu, izmantojot cauruli vai cilindru.
Saskaņā ar grieķu vēsturnieka Diodoro teikto, pateicoties šim izgudrojumam, tas atviegloja seno Ēģiptes auglīgo zemju, kas atrodas pie Nīlas upes, apūdeņošanu, jo tradicionālajiem instrumentiem vajadzēja milzīgu fizisku piepūli, kas izsmēja strādniekus.
Izmantotajam cilindram ir tāda paša garuma skrūve, kas uztur savstarpēji savienotu dzenskrūves vai spuras sistēmu, kas veic rotējošu kustību, ko virza ar rotējošu sviru..
Tādā veidā helīciji spēs virzīt jebkuru vielu no apakšas uz augšu, veidojot sava veida bezgalīgu ķēdi.
Arhimēda ķīlis
Arhimēda kārta vai dzelzs roka, kā tas ir zināms, bija viens no briesmīgākajiem šī matemātiķa radītajiem kara ieročiem, kas kļuva par svarīgāko romiešu iebrukumu sicīliešu aizsardzībai..
Saskaņā ar pētījumiem, ko veica Drexel universitātes profesori Chris Rorres (Matemātikas katedra) un Harijs Harris (Civilās celtniecības un arhitektūras katedra), tas bija liels svira, kurai bija piesaistīts āķis. ar ķēdi, kas no tās karājās.
Ar sviras palīdzību āķis tika manipulēts tā, lai tas nokristu pret ienaidnieka kuģi, un mērķis bija to piekabināt un pacelt tik lielā mērā, ka, atlaižot to, to varēja pilnīgi apgāzt, vai arī nokļūt krastā..
Rorres un Harris iepazīstināja ar simpoziju "Mašīnas un ārkārtas senlietu struktūras" (2001), miniatūras priekšstatu par šo artefaktu ar nosaukumu "milzīgs kara mašīna: Arhimēda dzelzs roku būvniecība un darbība"
Šī darba realizācijai viņi paļāvās uz seno vēsturnieku Polibio, Plutarco un Tito Livio argumentiem..
Atsauces
- ASSIS, A. (2008). Arhimēda, smaguma centrs, un pirmais mehānikas likums [tiešsaistē]. Piekļuve 2017. gada 10. jūnijam par bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [tiešsaistē]. Piekļuve 2015. gada 9. jūnijā World Wide Web: books.google.co.ve/books.
- MOLINA, A. (2008). Sirakūzas Arhimēda pētnieciskā metode: intuīcija, mehānika un izpēte [tiešsaistē]. Pieejams 2017. gada 10. jūnijā World Wide Webproduccioncientifica.luz.edu.
- O'CONNOR, J. & ROBERTSON, R. (1999). Arhimēda no Sirakūzas [tiešsaistē]. Piekļuve 2017. gada 9. jūnijam vietnē history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Arhimēda: viņa dzīve, darbi un iemaksas mūsdienu matemātikā [tiešsaistē]. Saturs iegūts 2017. gada 9. jūnijā vietnē lfunes.uniandes.edu.co.
- QUINN, L. (2005). Arhimēda no Sirakūzas [tiešsaistē]. Pieejams 2017. gada 9. jūnijā math.ucdenver.edu.
- RORRES, C. & HARRIS, H. (2001). Lielisks kara aparāts: Arhimēda dzelzs roku būvniecība un darbība [tiešsaistē]. Saturs saņemts 2017. gada 10. jūnijā vietnē cs.drexel.edu.
- VITE, L. (2014). Arhimēda princips [tiešsaistē]. Saturs iegūts 2017. gada 10. jūnijā vietnē repository.uaeh.edu.mx.


